First Graduate School in Mathematics
May 28–31, 2024
We invite Master's and PhD students from across the country, as well as advanced undergraduate students in Mathematics or Mathematical Engineering, to apply and take part in this academic event.
The purpose of the school is to strengthen the ties between undergraduate and graduate students in Mathematics and Statistics in Chile and neighboring countries.
The school will feature three short courses in Algebra and Geometry, Probability, and Analysis, taught by professors from various universities. Each course will consist of four sessions, approximately 50 minutes each. The first two sessions will be introductory, intended for all students and early-career researchers, while the last two will be more advanced, targeting students specializing in the area.
Additionally, there will be ten research talks delivered by postdoctoral researchers and graduate students.
Benefits for selected participants:
- Accommodation in shared cabins.
- Transportation from Temuco to Lican Ray, provided by university buses.
Location:
Lican Ray Recreational Center
Universidad de La Frontera
Application Results: Friday, May 3

Short Courses
|
ÁLGEBRA Y GEOMETRÍA |
|
| Título | Ida y vuelta de Álgebras a Variedades: el ejemplo de variedades tóricas. |
| Resumen | En este minicurso se describe la equivalencia clásica entre álgebras finitamente generadas y variedades afines con un enfoque computacional (uso del software MAGMA). En la primera parte del curso se explica como construir una variedad afín a partir de un ideal en un anillo de polinomios y viceversa. En la segunda parte se introducen las variedades tóricas afines y se muestra su equivalencia con algebras finitamente generadas asociadas a semigrupos. |
| Referencias | (1). Apuntes Andreas Gathmann https://agag-gathmann.math.rptu.de/en/alggeom.php (2). Toric Varieties, D. Cox, J. Little, H. Schenck (3). Algebraic Geometry, R. Hartshorne |
From algebras to varieties and back: The case of Toric varieties
Speakers:
Michela Artebani (Universidad de Concepción) and Paola Comparin (Universidad de La Frontera)
|
PROBABILIDADES |
|
| Título | Introducción a las Ecuaciones Diferenciales Estocásticas dirigidas por Movimiento Browniano y Aplicaciones |
| Resumen | El movimiento Browniano ha sido extensivamente estudiado desde su descubrimiento en el siglo XIX, y cuya descripción matemática se fundamenta en la teoría de los procesos estocásticos mediante el proceso de Wiener. El cálculo estocástico establece los fundamentos teóricos de la integración estocástica con respecto al movimiento Browniano. Las ecuaciones diferenciales estocásticas de Itô permiten modelar procesos de difusión a tiempo continuo definidos sobre un espacio de probabilidad completo y adaptados a una filtración. Las EDE se definen en un estado inicial, y evolucionan de acuerdo a sus términos de tendencia y los coeficientes de difusión dirigidos por movimiento Browniano. La fórmula de Feynman-Kac relaciona los sistemas de EDE con las ecuaciones diferenciales parciales, presentando una interpretación probabilística de las soluciones deterministas mediante valores esperados de funcionales integrales. Los sistemas de partículas estocásticas son modelados mediante sistemas de EDE que describen las trayectorias y propiedades dinámicas de las soluciones a través del tiempo, como por ejemplo, la posición y la velocidad de las partículas de un fluido en movimiento. El método de Euler-Maruyama aproxima numéricamente las soluciones exactas de EDE con coeficientes continuos, al discretizar los intervalos de tiempo e integrar localmente las ecuaciones. Para ello, se fija un tamaño de paso de discretización temporal y se simulan los incrementos de Wiener utilizando variables aleatorias Gaussianas. La simulación computacional de las EDE utiliza soluciones numéricas cuyo análisis involucra teoremas de existencia y unicidad, convergencia, propiedades de estabilidad, estimación de esperanzas matemáticas y generación de variables aleatorias. Se presentarán aplicaciones relacionadas a la solución numérica débil de EDE, a través de la implementación computacional de metodologías probabilísticas. En particular, se presentarán esquemas numéricos en el contexto del movimiento Browniano geométrico. Además, se expondrán métodos de estimación para la solución numérica de EDP no lineales. |
Introduction to stochastic differential equations driven by Brownian motion and applications
Speaker:
Hernán Mardones González (Universidad de La Frontera)
|
ANÁLISIS |
|
| Título | Introducción al Análisis Semiclásico |
| Resumen | En este cursillo introduciremos las principales herramientas y temáticas del análisis semiclásico en el contexto de la teoría espectral de Hamiltonianos cuánticos. El objetivo es poder presentar un resultado famoso sobre la distribución asíıntotica de valores propios discretos en el régimen semiclásico conocido como la ley de Weyl. El plan del cursillo es el siguiente: Sesión I: Teoría espectral y mecánica cuántica (Operadores acotados y no–acotados en espacios de Hilbert, teorema espectral para operadores autoadjuntos, observables cuánticos y ecuación de Schrödinger) Sesión II: Cuantización y operadores pseudodiferenciales: (Clases de símbolos y cálculo pseudodiferencial) Sesión III: Cálculo funcional pseudodiferencial estacionario: (Fórmula de Helffer–Sjöstrand, fórmula de traza semiclásica) Sesión IV: Aplicación del cálculo funcional pseudodiferencial al estudio del espectro discreto (Ley de Weyl). |
| Referencias | (1) M. Dimassi and J. Sjöstrand. Spectral Asymptotics in the Semi-Classical Limit. London Mathematical Society Lecture Note Series 268. (2) A. Martinez. An Introduction to Semiclassical and Microlocal Analysis. Universitext, Springer, 2002. (3) M. Zworski. Semiclassical Analysis. Graduate Studies in Math. 138, Amer. Math. Soc., 2012. |
Introduction to semiclassical analysis
Profesores Responsables:
Marouane Assal (Universidad de Santiago de Chile) and Daniel Parra (Universidad de La Frontera)
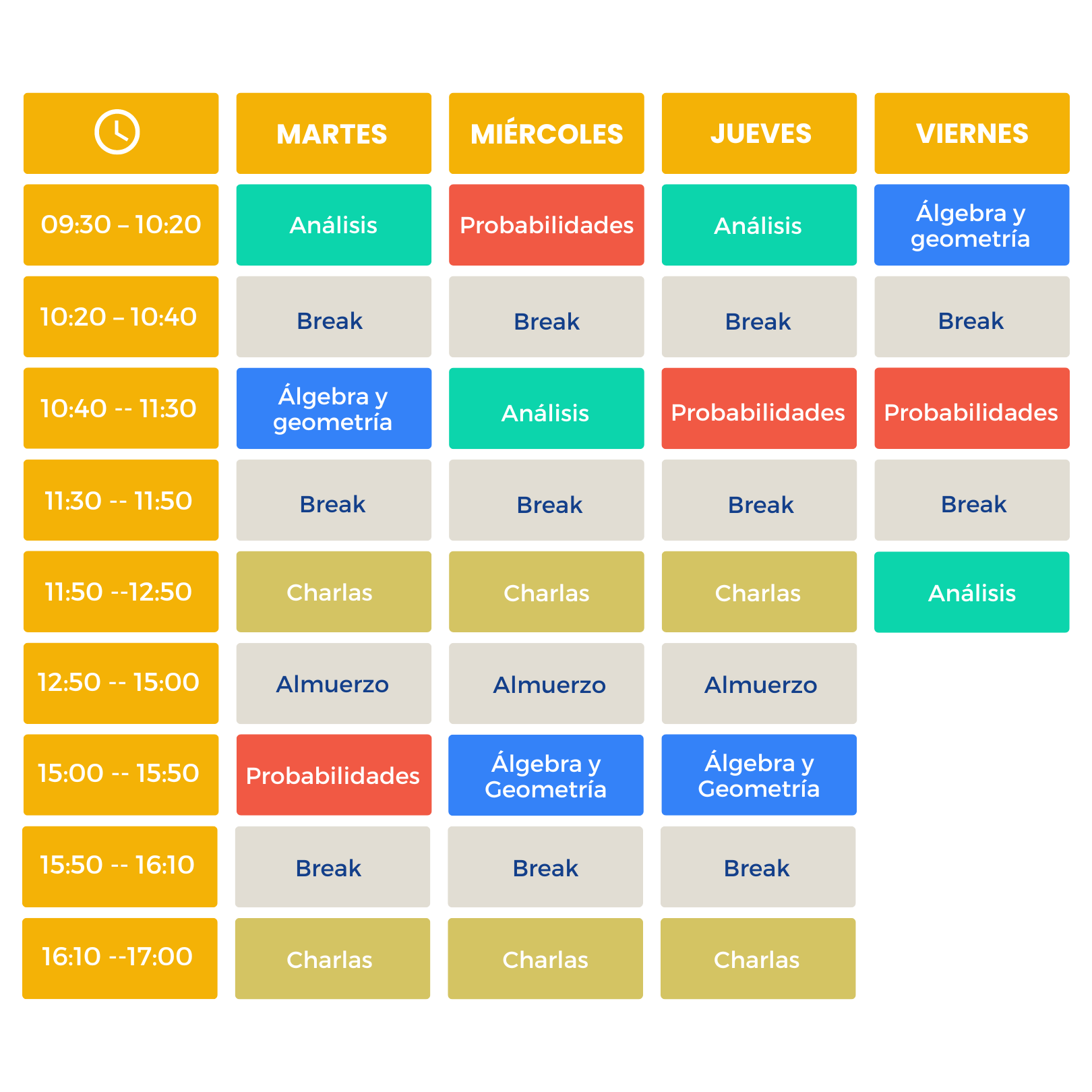
Program
Academic Talks
Tuesday 28
Israel Morales
Universidad de La Frontera
Title:
The geometry of groups: a large-scale perspective
Wednesday 29
Manuel González-Navarrete
Universidad de La Frontera
Title:
On the asymptotic of a lazy reinforced random walk
Thursday 30
Saúl Quispe
Universidad de La Frontera
Title:
Field of moduli vs fields of definition of rational functions
Student Talks
Gonzalo Rodríguez
Universidad de Talca
Title:
Simultaneous resolution of degenerate μ-constant deformations
Fabián Caro
Universidad de Antofagasta
Title:
Generalized symmetries of the centrally charged membrane
Víctor Valdebenito
Universidad de La Frontera
Title:
Prym-Tyurin varieties as isotypical components of a Jacobian variety
Nicanor Carrasco Vargas
Pontificia Universidad Católica de Chile
Title:
Algorithmic undecidability of dynamical properties of $\mathbb{Z}^2$-Tilings, SFTs, and their topological factors
Pablo Alvarado
Universidad de Chile
Title:
Representations of groups of automorphisms on compact Riemann surfaces
Lesly Suarez Diaz
Universidad de Santiago de Chile
Title:
Construction of Abelian extensions of quadratic fields
Victor Valencia Hernández
Pontificia Universidad Católica de Chile
Title:
Frankel and wilking theorems
Tobías Martínez
Universidad Técnica Federico Santa María
Title:
Ulrich bundles over Hirzebruch surfaces




Organizing Team
Paola Comparin
María Elisa Valdés
Saúl Quispe
Ángel Carocca
Doctoral Program in Mathematical Sciences
Universidad de La Frontera
Temuco, Chile




